[Study Notes] Trigonometric Functions (Sine, Cosine, Tangent)

The sine function and cosine function are the two most fundamental and significant functions in trigonometry. They have extensive applications in describing periodic phenomena, oscillations, vibrations, rotations, and more. Below is a detailed introduction to the sine and cosine functions.

Sine Function

Definition

For an angle \theta, the sine function \sin(\theta) is defined as the (y)-coordinate of the point corresponding to the angle on the unit circle. The unit circle is a circle with a radius of 1 and its center at the origin.

Expression

Properties

1. Periodicity: The sine function is a periodic function with a period of 2\pi:

   \sin(\theta + 2k\pi) = \sin(\theta)

   where (k) is any integer.

2. Odd Function: The sine function is an odd function:

   \sin(-\theta) = -\sin(\theta)

3. Range: The range of the sine function is [-1, 1].

4. Special Values:

   \sin(0) = 0
   \sin\left(\frac{\pi}{2}\right) = 1
   \sin(\pi) = 0
   \sin\left(\frac{3\pi}{2}\right) = -1
   \sin(2\pi) = 0

Graph

The graph of the sine function is a sine wave oscillating above and below the (x)-axis.

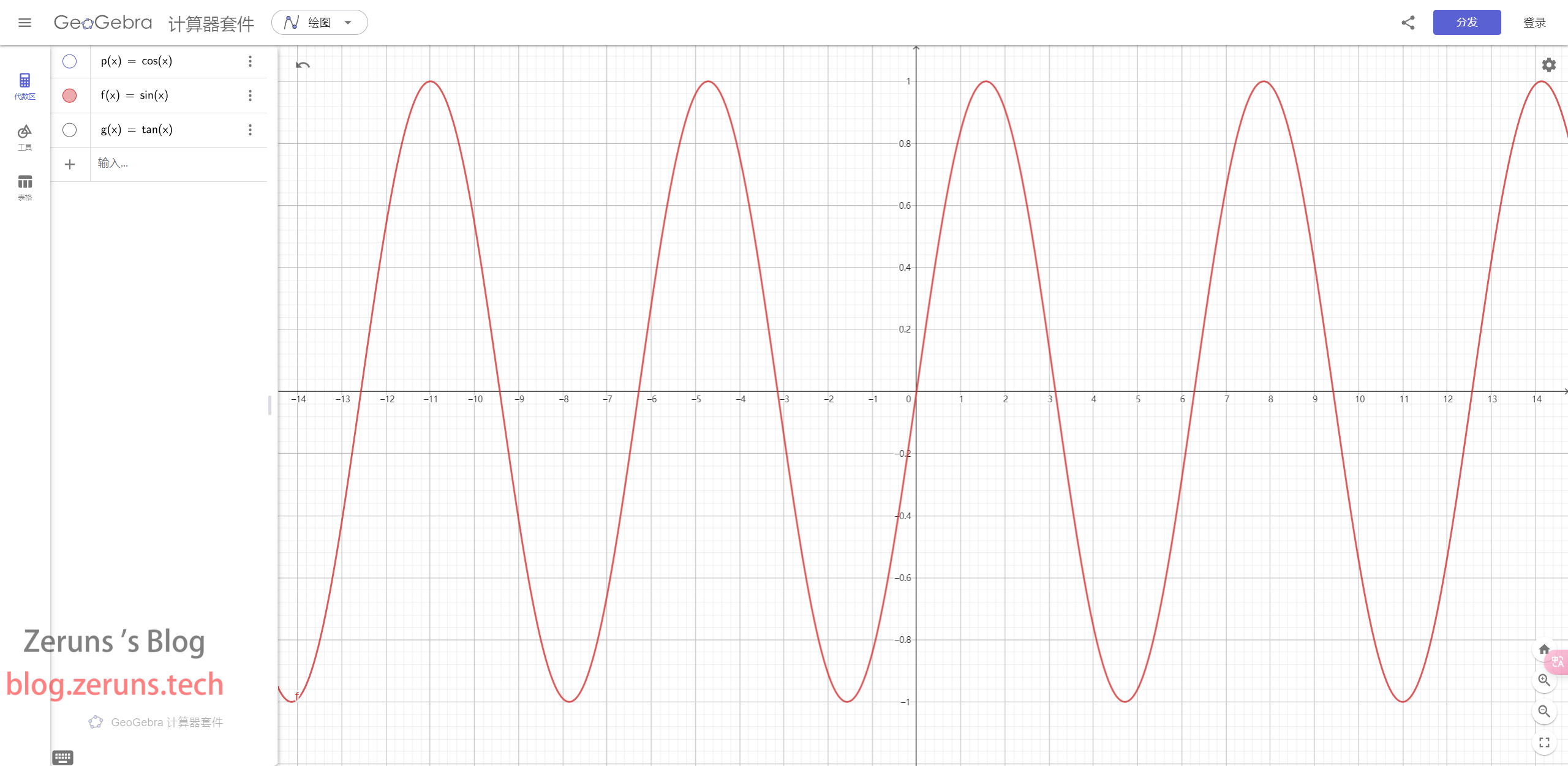
Cosine Function

Definition

For an angle \theta, the cosine function \cos(\theta) is defined as the (x)-coordinate of the point corresponding to the angle on the unit circle.

Expression

Properties

1. Periodicity: The cosine function is a periodic function with a period of 2\pi:

   \cos(\theta + 2k\pi) = \cos(\theta)

   where (k) is any integer.

2. Even Function: The cosine function is an even function:

   \cos(-\theta) = \cos(\theta)

3. Range: The range of the cosine function is [-1, 1].

4. Special Values:

   \cos(0) = 1
   \cos\left(\frac{\pi}{2}\right) = 0
   \cos(\pi) = -1
   \cos\left(\frac{3\pi}{2}\right) = 0
   \cos(2\pi) = 1

Graph

The graph of the cosine function is a wave symmetric about the (y)-axis, similar to the sine wave but with a phase shift.

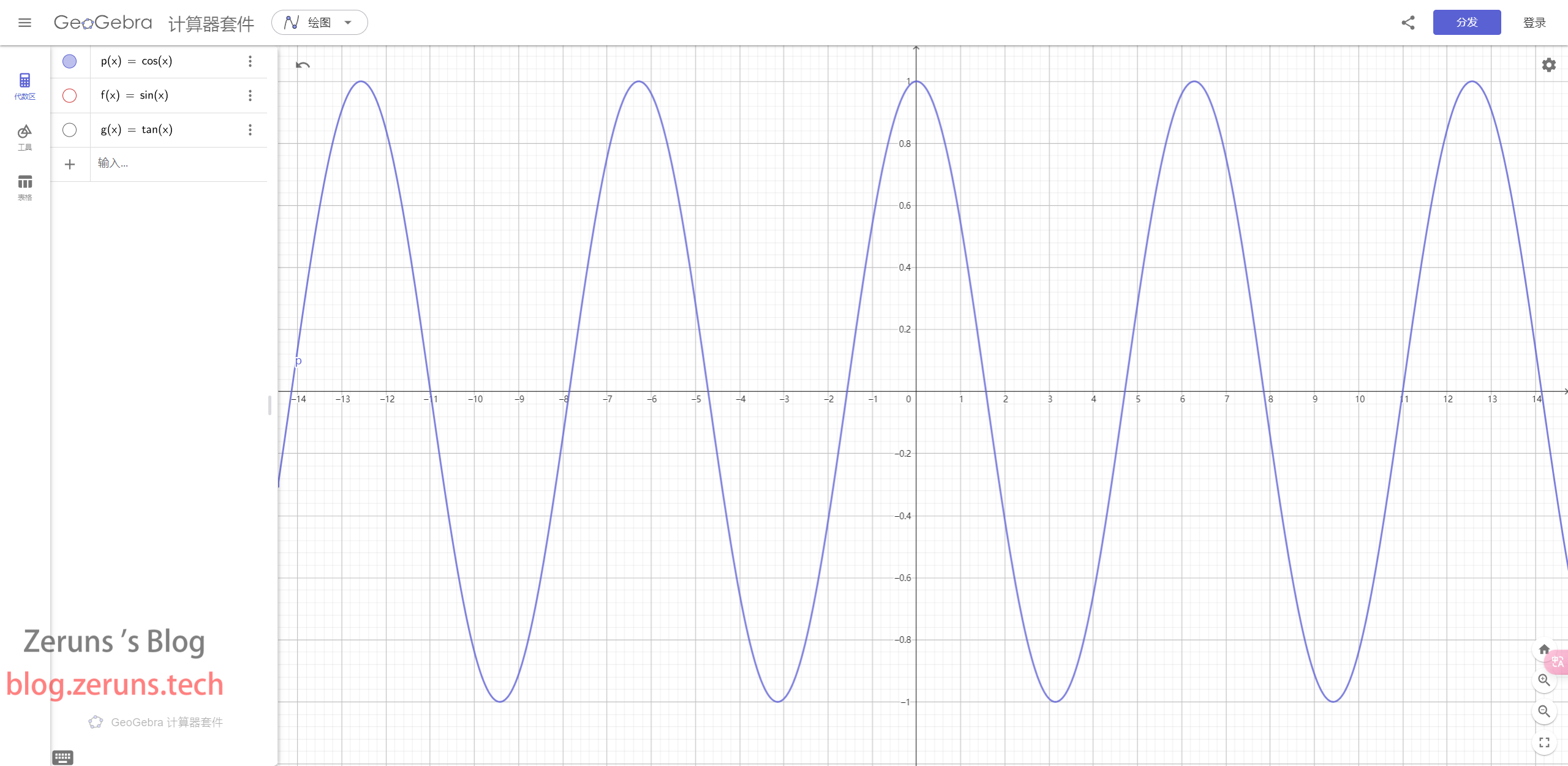
Relationships Between the Sine and Cosine Functions

There are many important relationships between the sine and cosine functions, including:

1. Phase Difference:

   \sin(\theta) = \cos\left(\theta - \frac{\pi}{2}\right)
   \cos(\theta) = \sin\left(\theta + \frac{\pi}{2}\right)

2. Pythagorean Identity:

   \sin^2(\theta) + \cos^2(\theta) = 1

3. Sum and Difference Formulas:

   \sin(\alpha \pm \beta) = \sin(\alpha)\cos(\beta) \pm \cos(\alpha)\sin(\beta)
   \cos(\alpha \pm \beta) = \cos(\alpha)\cos(\beta) \mp \sin(\alpha)\sin(\beta)

4. Double-Angle Formulas:

   \sin(2\theta) = 2\sin(\theta)\cos(\theta)
   \cos(2\theta) = \cos^2(\theta) - \sin^2(\theta)

5. Auxiliary Angle Formulas:

   \sin(\theta) = \pm \sqrt{1 - \cos^2(\theta)}
   \cos(\theta) = \pm \sqrt{1 - \sin^2(\theta)}

Applications

The sine and cosine functions have wide-ranging applications in various fields, including but not limited to:

• Physics: Describing waves, vibrations, and harmonics.
• Engineering: Signal processing, communications, and control systems.
• Astronomy: Modeling the orbits of planets and satellites.
• Biology: Representing periodic biological phenomena such as heartbeat and respiration.

The sine and cosine functions are also foundational concepts in trigonometry and Fourier analysis, used to analyze and process periodic phenomena.

Tangent Function

The tangent function is one of the fundamental trigonometric functions. It has wide applications in mathematics, physics, and engineering. Below is a detailed introduction to the tangent function.

Definition of the Tangent Function

The tangent function \tan(\theta) is defined as the ratio of the sine function \sin(\theta) to the cosine function \cos(\theta):

Properties of the Tangent Function

1. Domain: The tangent function is undefined where the cosine function equals zero, that is:

where k is any integer.

2. Range: The range of the tangent function is all real numbers (-\infty, \infty).
3. Periodicity: The tangent function is periodic with a period of \pi:

where k is any integer.

4. Parity: The tangent function is an odd function:

5. Special Values:
   • \tan(0) = 0
   • \tan\left(\frac{\pi}{4}\right) = 1
   • \tan\left(\frac{\pi}{2}\right) is undefined
   • \tan\left(\frac{3\pi}{4}\right) = -1

Graph of the Tangent Function

The graph of the tangent function is a waveform with a period of \pi. It has vertical asymptotes at \theta = \frac{\pi}{2} + k\pi, where k is any integer. At these points, the value of the tangent function approaches positive or negative infinity.

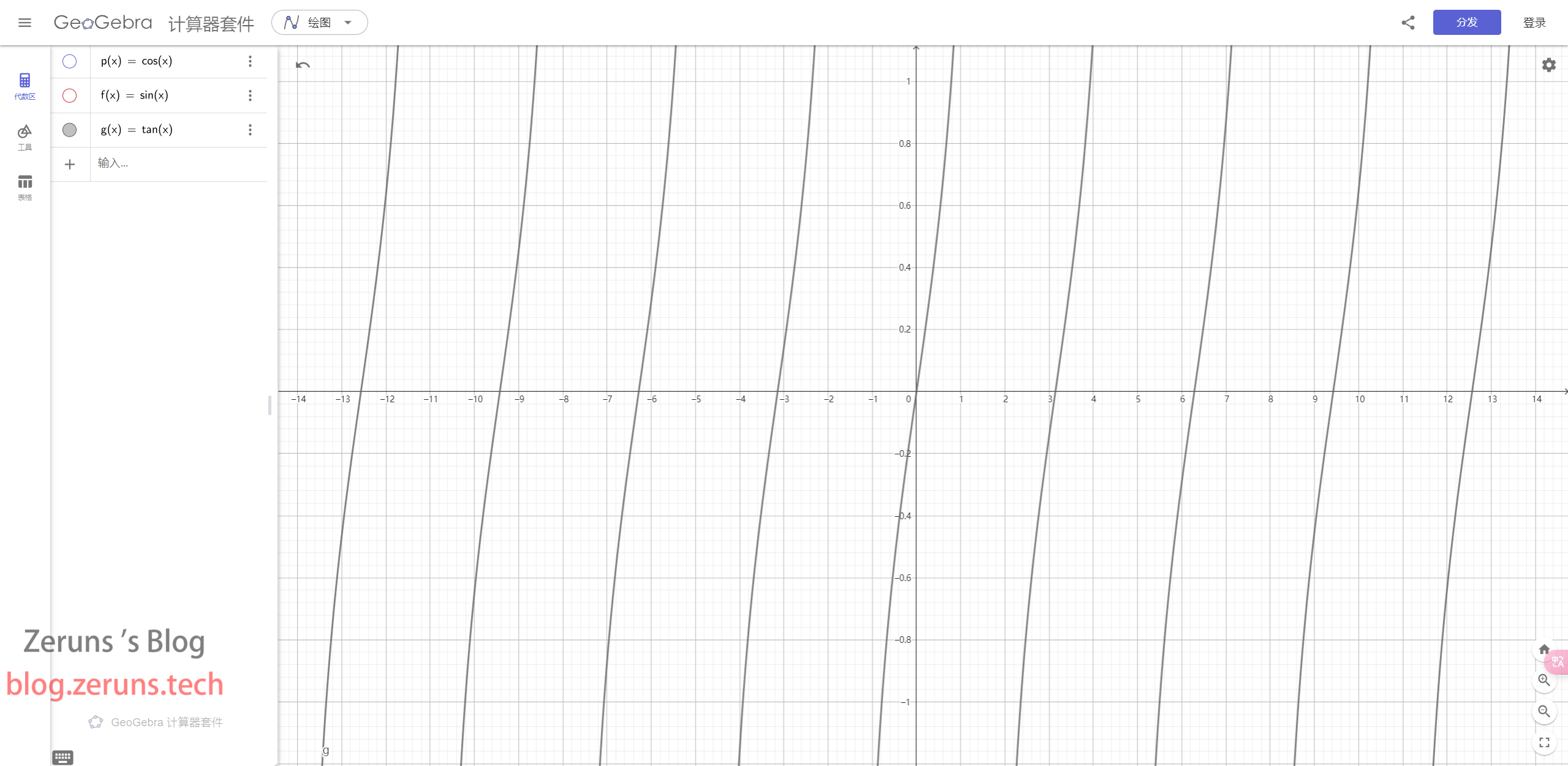
Relationships Between the Tangent Function and Other Trigonometric Functions

The tangent function has several important relationships with other trigonometric functions, including:

1. Basic Definition:

   \tan(\theta) = \frac{\sin(\theta)}{\cos(\theta)}

2. Reciprocal Relationship:

   \cot(\theta) = \frac{1}{\tan(\theta)} = \frac{\cos(\theta)}{\sin(\theta)}

   where \cot(\theta) is the cotangent function.

3. Pythagorean Identity:

   \sec^2(\theta) = 1 + \tan^2(\theta)

   where \sec(\theta) = \frac{1}{\cos(\theta)} is the secant function.

4. Sum and Difference Formulas:

   \tan(\alpha \pm \beta) = \frac{\tan(\alpha) \pm \tan(\beta)}{1 \mp \tan(\alpha)\tan(\beta)}

5. Double-Angle Formula:

   \tan(2\theta) = \frac{2\tan(\theta)}{1 - \tan^2(\theta)}

Applications of the Tangent Function

The tangent function is applied in various fields, particularly in the following areas:

• Geometry: In a right triangle, the tangent function represents the ratio of the length of the opposite side to the adjacent side.
• Physics: Used to describe waves, vibrations, and slopes.
• Engineering: Utilized in signal processing, communications, and control systems to analyze and process periodic signals.
• Navigation and Astronomy: Helps calculate angles and distances.

Conclusion

The tangent function is a periodic function with many significant properties and applications. Understanding and mastering the tangent function is crucial for solving various mathematical and engineering problems.

Graphs of the Three Functions

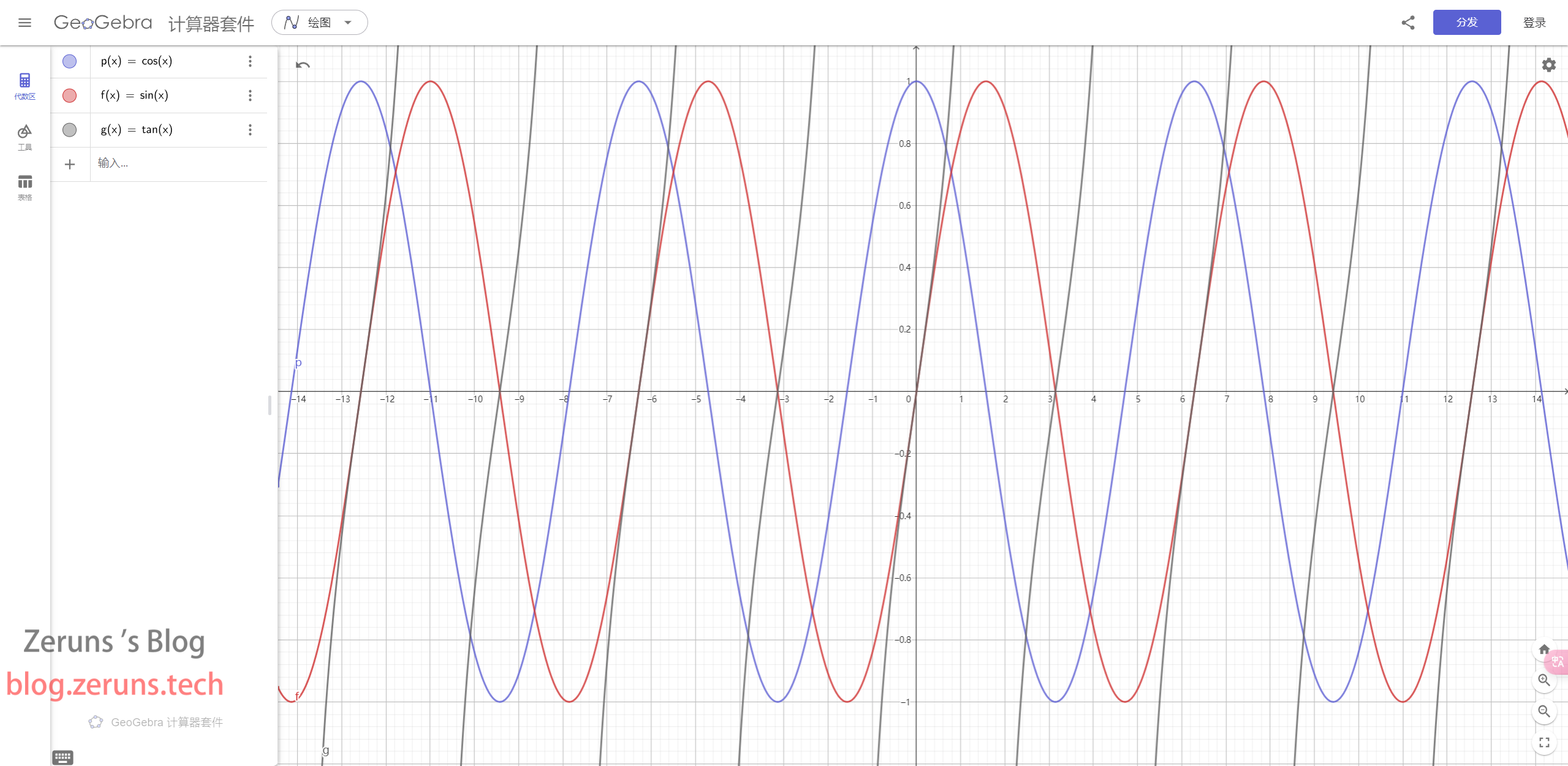
Recommended Articles

• Cost-Effective and Affordable VPS/Cloud Server Recommendations: https://blog.zeruns.tech/archives/383.html
• Minecraft Server Setup Tutorial: https://blog.zeruns.tech/tag/mc/
• Disassembly and Analysis of the Radeis D1500 Uninterruptible Power Supply (UPS): https://blog.zeruns.tech/archives/792.html
• Open Source Synchronous Rectification Buck-Boost Digital Power Supply Based on STM32: https://blog.zeruns.tech/archives/791.html
• Review and Image Quality Test of UNI-T UTi261M Thermal Imaging Camera: https://blog.zeruns.tech/archives/798.html
• Open Source 140W+65W Buck-Boost PD3.1 Fast Charging Module (2C+1A Ports), IP6557+IP6538, 205W Desktop Charger: https://blog.zeruns.tech/archives/801.html

Disclaimer

This article is AI-generated and has been manually reviewed for accuracy.